Dự báo tăng trưởng kinh tế Việt Nam năm 2025: So sánh mô hình GARCH và MIDAS1

ThS. Phạm Thành Công - Viện Kinh tế Việt Nam; Email: congth98@yahoo.com

TS. Lý Đại Hùng - Viện Kinh tế Việt Nam

Tóm tắt

Bài viết dự báo tăng trưởng kinh tế Việt Nam năm 2025 thông qua 2 mô hình GARCH và MIDAS. Kết quả so sánh cho thấy, mô hình GARCH đã chứng tỏ sự ưu việt hơn trong khả năng dự báo tăng trưởng so với mô hình MIDAS.

Từ khóa: dự báo, tăng trưởng, Việt Nam, GARCH, MIDAS

Abstract

The study focuses on analyzing the forecast of Vietnam's economic growth in 2025 through two models GARCH and MIDAS. The forecast results show that the GARCH model has proven to be superior in providing more accurate forecasts than the MIDAS model.

Keywords: forecast, economic growth, Vietnam, GARCH, MIDAS

ĐẶT VẤN ĐỀ

Trong bối cảnh kinh tế toàn cầu đầy biến động và khó lường, việc dự báo tốc độ tăng trưởng kinh tế trở thành một yếu tố then chốt để đưa ra các chính sách kinh tế phù hợp. Tăng trưởng kinh tế, trong khuôn khổ bài viết này, được đo lường bởi tốc độ gia tăng tổng sản lượng (GDP) giá so sánh theo thời gian, là chỉ tiêu phản ánh sức khỏe của nền kinh tế và ảnh hưởng trực tiếp đến các quyết định đầu tư, chi tiêu công và chính sách tài khóa, tiền tệ khác. Đối với các nhà hoạch định chính sách, dự báo chính xác tăng trưởng kinh tế giúp xác định các xu hướng kinh tế trong tương lai, từ đó đưa ra các biện pháp điều chỉnh kịp thời nhằm ổn định và thúc đẩy tăng trưởng kinh tế. Đối với các doanh nghiệp và nhà đầu tư, dự báo chính xác tăng trưởng kinh tế cung cấp thông tin quan trọng để lập kế hoạch kinh doanh và đầu tư, từ đó giảm thiểu rủi ro và tối đa hóa lợi nhuận.

Trong thực tế có nhiều phương pháp và mô hình nhằm dự báo tăng trưởng kinh tế, trong đó 2 mô hình GARCH và MIDAS được nhiều nghiên cứu sử dụng nhằm dự báo tăng trưởng kinh tế.

Đối với mô hình GARCH, một số nghiên cứu điển hình, như: Nguyễn Thanh Hương và Bùi Quang Trung (2015) dự báo chỉ số VN-Index trong giai đoạn 04/08/2014 đến ngày 21/11/2014; Lê Văn Tuấn và Phùng Duy Quang (2020) dự báo ảnh hưởng của dịch Covid-19 đến thị trường chứng khoán Việt Nam; Nguyễn Thị Hiên và cộng sự (2022) phân tích độ biến động của hợp đồng tương lai VN30F1M trên thị trường chứng khoán phái sinh Việt Nam; Phùng Duy Quang và cộng sự (2024) ứng dụng mô hình GARCH dự báo giá gạo Thái Lan.

Đối với mô hình MIDAS, một số nghiên cứu điển hình như Trần Minh Quân (2021) về dự báo lạm phát ở Việt Nam, cho thấy rằng mô hình MIDAS cung cấp dự báo chính xác hơn so với các mô hình truyền thống, với hai chỉ số về MAE và RMSE thấp hơn đáng kể. Nguyễn Thanh Tùng và Phạm Thị Lan Anh (2022) sử dụng mô hình MIDAS để dự báo tăng trưởng của Việt Nam, kết hợp dữ liệu hàng ngày về tỷ giá hối đoái và lãi suất với dữ liệu GDP hàng quý từ năm 2010 đến năm 2021. Kết quả ghi nhận mô hình MIDAS không chỉ cải thiện độ chính xác của dự báo mà còn cung cấp các thông tin hữu ích cho việc ra quyết định chính sách; Lê Mai Trang và cộng sự (2022) dự báo tăng trưởng GDP của Việt Nam dựa trên bộ số liệu thu thập từ năm 2006- 2020 thông qua 2 mô hình là MIDAS và MF-VAR. Kết quả nghiên cứu thực nghiệm cho thấy, mô hình MIDAS cho kết quả dự báo tốt hơn so với mô hình MF-VAR.

Nhìn chung, việc dự báo nền kinh tế nói chung và chỉ số tăng trưởng kinh tế nói riêng luôn được nhiều nhà nghiên cứu quan tâm. Tuy vậy, các nghiên cứu so sánh 2 mô hình GARCH và MIDAS để dự báo tăng trưởng kinh tế là tương đối hạn chế. Do đó, bài nghiên cứu này sẽ đóng góp thêm một phần luận điểm mới về dự báo tăng trưởng.

CƠ SỞ LÝ THUYẾT

Mô hình MIDAS (Mixed Data Sampling)

Mô hình MIDAS (Mixed Data Sampling) là một phương pháp tiên tiến cho phép kết hợp dữ liệu có tần suất khác nhau để dự báo một biến số. MIDAS được thiết kế để tận dụng thông tin từ các biến số tần suất cao (như dữ liệu hàng ngày) để dự báo các biến số tần suất thấp (như GDP hàng quý), giúp cải thiện độ chính xác của dự báo bằng cách khai thác các biến động ngắn hạn từ dữ liệu tần suất cao.

Phương trình MIDAS tổng quát có dạng như sau:

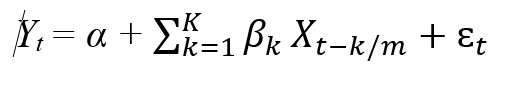Trong đó:

Yt là giá trị của chuỗi thời gian tại thời điểm t.

Xt - k/m là giá trị của biến tần suất cao tại thời điểm t−k/m.

α là hằng số.

k là các hệ số của biến tần suất cao.

i là nhiễu trắng tại thời điểm t.

K là độ trễ tối đa.

m là tần suất của dữ liệu cao so với dữ liệu thấp.

Mô hình GARCH (Generalized Autoregressive Conditional eteroskedasticity)

Mô hình GARCH do Bollerslev (1986) phát triển dựa trên mô hình ARCH (Autoregressive Conditional Heteroskedasticity) của Engle (1982), là một trong những phương pháp phổ biến để phân tích và dự báo biến động trong các chuỗi thời gian kinh tế và tài chính. Mô hình này được sử dụng rộng rãi để đo lường sự biến động có điều kiện, đặc biệt trong dữ liệu tài chính, như: giá cổ phiếu, lãi suất hoặc tỷ giá hối đoái.

Mô hình GARCH (p, q) được định nghĩa bởi 2 phương trình:

Thứ nhất, phương trình hồi quy tuyến tính (mô tả biến phụ thuộc):

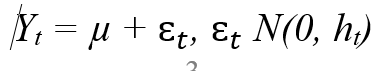Trong đó:

Yt là biến phụ thuộc tại thời điểm t

µ là giá trị trung bình hoặc kỳ vọng của Yt

€t là thành phần nhiễu (sai số) có phương sai điều kiện ht

Thứ hai, phương trình phương sai điều kiện (mô tả sự biến động):

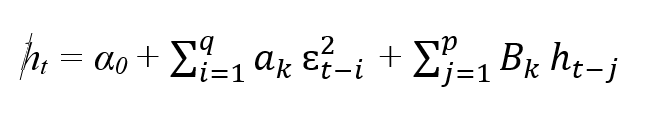Trong đó:

ht là phương sai có điều kiện tại thời điểm t

α0 là hằng số, thể hiện phương sai tối thiểu (nếu không có các yếu tố khác).

€2t-1 là sai số bình phương tại các thời điểm trước, phản ánh tin tức mới

ht-j là hương sai có điều kiện tại các thời điểm trước đó, phản ánh tính dai dẳng của biến động.

(q, p) là các bậc của thành phần ARCH và GARCH.

Đánh giá hiệu quả mô hình GARCH và MIDAS

Bài viết sử dụng 2 chỉ số chính để đánh giá độ chính xác của các mô hình dự báo, bao gồm sai số bình phương trung bình (RMSE), sai số tuyệt đối trung bình (MAE). Trong đó, RMSE được tính bằng căn bậc hai của giá trị trung bình các bình phương sai lệch giữa giá trị dự báo và giá trị thực tế. Chỉ số này tập trung vào việc làm nổi bật các sai lệch lớn hơn, nhờ vào việc bình phương các sai số và được sử dụng phổ biến để đo lường hiệu quả của các mô hình dự báo.

PHƯƠNG PHÁP NGHIÊN CỨU

Phương pháp dự báo bằng mô hình GARCH

Phần lớn chuỗi thời gian không dừng, trong khi mô hình GARCH yêu cầu tính dừng. Một chuỗi được xem là dừng nếu trung bình và phương sai không đổi theo thời gian, và đồng phương sai chỉ phụ thuộc vào khoảng cách thời gian. Tính dừng được kiểm tra qua: đồ thị chuỗi thời gian, hàm tự tương quan mẫu (SACF), kiểm định Dickey –Fuller. Nếu chuỗi không dừng, thực hiện sai phân để làm dừng. Nhận dạng mô hình GARCH (p, d, q) là bước xác định các giá trị phù hợp cho 3 tham số: p (bậc tự hồi quy); d (bậc sai phân); và q (bậc trung bình trượt). Thông thường, d được xác định bằng cách kiểm tra và thực hiện sai phân để làm dừng chuỗi thời gian nếu cần thiết.

Sau đó, giá trị của p và q được lựa chọn dựa trên đồ thị của hàm tự tương quan mẫu (SACF) và hàm tự tương quan mẫu riêng phần (SPACF). Cụ thể, p được xác định khi đồ thị SPACF có giá trị lớn tại các độ trễ từ 1 đến p và giảm mạnh sau đó, đồng thời SACF giảm dần. Tương tự, q được xác định nếu đồ thị SACF có giá trị lớn tại các độ trễ từ 1 đến q và giảm mạnh sau đó, trong khi SPACF giảm dần. Phương pháp này giúp xác định cấu trúc tối ưu để mô hình hóa phương sai biến động của chuỗi thời gian. Sau khi loại bỏ xu hướng, kiểm tra sự tồn tại của phương sai có điều kiện (heteroskedasticity) bằng kiểm định ARCH. Nếu tồn tại, sử dụng mô hình GARCH để mô hình hóa phương sai biến đổi qua thời gian. Ước lượng các tham số của mô hình bằng phương pháp Maximum Likelihood Estimation (MLE). Sau đó, đánh giá mô hình bằng cách kiểm tra phần dư (residuals) và phương sai có điều kiện để đảm bảo không còn cấu trúc trong dữ liệu chưa được giải thích. Sử dụng mô hình đã được hiệu chỉnh để dự báo phương sai có điều kiện trong tương lai. Từ đó, ước tính mức độ biến động của các biến tài chính và đánh giá rủi ro.

Phương pháp dự báo bằng mô hình MIDAS

Xác định mô hình MIDAS là bước quan trọng trong quy trình. Đầu tiên, lựa chọn các biến tần suất cao có thể ảnh hưởng đến biến tần suất thấp. Sau đó, xác định biến tần suất thấp cần phải dự báo, cụ thể là GDP hàng quý. Mô hình MIDAS yêu cầu thiết lập một hàm trọng số để kết hợp dữ liệu tần suất cao và thấp. Các hàm trọng số phổ biến bao gồm: hàm polynomial; hàm exponential; và hàm spline, mỗi loại có những đặc điểm riêng giúp mô hình hóa mối quan hệ giữa dữ liệu tần suất cao và thấp. Ước lượng mô hình MIDAS liên quan đến việc xác định các tham số của mô hình sao cho mô hình có thể phản ánh chính xác mối quan hệ giữa dữ liệu tần suất cao và dữ liệu tần suất thấp. Để thực hiện việc này, các phương pháp tối ưu hóa thường được sử dụng, chẳng hạn như: ước tính độ tin cậy tối đa (MLE) hoặc phương pháp Bình phương nhỏ nhất.

KẾT QUẢ NGHIÊN CỨU VÀ THẢO LUẬN

Kiểm định mô hình GARCH để dự báo tốc độ tăng trưởng kinh tế

Sau khi tiến hành kiểm định chuỗi dừng của tăng trưởng kinh tế và kiểm tra sự tồn tại của phương sai có điều kiện (heteroskedasticity) bằng kiểm định ARCH, thì mô hình GARCH phù hợp là (1,0) và kết quả hồi quy được thể hiện ở Bảng 1.

Bảng 1: Kết quả hồi quy mô hình GARCH (1,0)

Biến	Hệ số chặn	Độ lệch chuẩn	Thống kê z	Xác suất
C	5,583898	0,142034	39,31389	0
AR(5)	0,170771	0,072514	2,354998	0,0185

Nguồn: Ước lượng của nhóm tác giả

Kết quả mô hình GARCH (1,0) cho thấy, tất cả các hệ số đều có ý nghĩa thống kê (Bảng 1). Nhưng, để mô hình có độ tin cậy và có thể dùng để dự báo, thì cần thực hiện kiểm tra tính dừng của phần dư và hiệu ứng ARCH của mô hình GARCH (1,0).

Bảng 2: Kết quả kiểm tra tính dừng của chuỗi phần dư

		Thống kê t	Xác suất
Kiểm định Dickey-Fuller mở rộng (ADF)		-7.4244	0,0000
Kiểm định các giá trị	Mức 1%	-3,5482
	Mức 5%	-2,9126
	Mức 10%	-2,5940

Nguồn: Ước lượng của nhóm tác giả

Kết quả Bảng 2 kiểm tra tính dừng của chuỗi phần dư thông qua kiểm định ADF cho thấy chuỗi đạt tính dừng. Giá trị t-statistic là -7,4244, thấp hơn đáng kể so với các giá trị tới hạn ở mức 1%, 5%, và 10% (-3,5482; -2,9126; và -2,5940). Đồng thời, xác suất p-value là 0,0000, nên có mức ý nghĩa cao và bác bỏ giả thuyết H0​ (chuỗi không dừng). Điều này xác nhận rằng, chuỗi phần dư đã loại bỏ được xu hướng và tính không dừng, phù hợp để sử dụng trong các phân tích tiếp theo hoặc làm đầu vào cho các mô hình dự báo.

Bảng 3: Kiểm định phương sai sai số thay đổi của mô hình GARCH (1,0)

Kiểm định mô hình ARCH
Thống kê F	0,012421	Xác suất F(1,51)		0,9117
Biến	Hệ số chặn	Độ lệch chuẩn	Thống kê t	Xác suất
C	1,03456	0,402956	2,567426	0,0132
WGT_RESID^2(-1)	-0,015589	0,139873	-0,111449	0,9117

Nguồn: Ước lượng của nhóm tác giả

Kết quả Bảng 3 kiểm định phương sai sai số thay đổi của mô hình GARCH (1,0) thông qua kiểm định ARCH chỉ ra rằng, không có bằng chứng về hiện tượng phương sai thay đổi trong phần dư. Giá trị F-statistic là 0,012421 với xác suất là 0,9117. Cả 2 giá trị đều > 0,05, dẫn đến việc không bác bỏ giả thuyết gốc H0 (không có phương sai thay đổi). Điều này khẳng định thêm rằng, mô hình GARCH(1,0) đã loại bỏ được hiện tượng phương sai sai số thay đổi và phần dư của mô hình không còn chứa thông tin về phương sai điều kiện. Như vậy, mô hình có thể được coi là phù hợp về mặt xử lý phương sai.

Bảng 4: Kết quả dự báo GARCH (1,0)

Quý/năm	Dự báo
2025Q1	6,777911401
2025Q2	6,596893993
2025Q3	6,81377334
2025Q4	6,894035776
Trung bình năm 2025	6,770653628

Nguồn: Ước lượng của nhóm tác giả

Thông qua mô hình hồi quy GARCH (1,0), nghiên cứu đã thực hiện dự báo chỉ số tăng trưởng kinh tế của Việt Nam trong năm 2025 là 6,77% (Bảng 4). Điều này có thể phản ánh kỳ vọng của nền kinh tế Việt Nam vào năm 2025 sẽ duy trì mức tăng trưởng ổn định sau những ảnh hưởng của các yếu tố ngoại cảnh trong những năm trước đó.

Kiểm định mô hình MIDAS để dự báo tăng trưởng kinh tế

Bảng 5: Kết quả hồi quy MIDAS của tăng trưởng kinh tế với chỉ số sản xuất ngành công nghiệp đóng vai trò biến số tác động

Biến	Hệ số chặn	Độ lệch chuẩn	Thống kê t	Xác suất
C	4,2096	0,8799	4,7839	0,0000
GDPGROWTH (-1)	0,1971	0,1407	1,4011	0,1676
IIPINDUSTRIAL_PRODUCTION (-1)	0,1711	0,1429	1,1972	0,2371

Nguồn: Ước lượng của nhóm tác giả

Kết quả Bảng 5 cho thấy, hằng số đạt khoảng 4,2096 và độ trễ của tăng trưởng kinh tế đạt khoảng 0,1971, nhưng giá trị thống kê lại không đáng kể ở mức 10% với Prob đạt 0,1676.

Bảng 6: Dự báo tăng trưởng kinh tế bằng mô hình MIDAS

Quý/Năm	Dự báo
2025Q1	6,6413
2025Q2	6,1973
2025Q3	6,3373
2025Q4	6,5405
Trung bình năm 2025	6,4291

Nguồn: Ước lượng của nhóm tác giả

Kết quả Bảng 6 cho thấy, năm 2025 trung bình tăng trưởng kinh tế được dự báo đạt khoảng 6,43%, phản ánh một năm tăng trưởng ổn định, nhưng có thể đối mặt với những yếu tố tác động tiêu cực hoặc sự không chắc chắn trong các quý đầu năm. Như vậy, khi so sánh Bảng 6 với Bảng 5, thì kết quả dự báo của mô hình MIDAS thấp hơn so với mô hình GARCH về tăng trưởng kinh tế năm 2025.

Sự khác biệt về kết quả dự báo phản ánh sự khác biệt trong cấu trúc của 2 mô hình. Mô hình GARCH chú trọng vào khả năng thay đổi của phương sai sai số của tăng trưởng kinh tế tại Việt Nam. Bởi vậy, mô hình này tập trung vào biến động của chính tăng trưởng theo thời gian, nhất là khả năng thay đổi hình thái của sai số. Trong khi đó, mô hình MIDAS có khả năng nắm bắt các yếu tố tác động đến nền kinh tế theo các tần suất khác nhau, gồm các yếu tố tác động ngắn hạn hay dài hạn và các yếu tố vĩ mô có thể thay đổi nhanh hay chậm.

So sánh mô hình MIDAS và GARCH

Khi so sánh hiệu suất của 2 mô hình dự báo MIDAS và GARCH dựa trên các chỉ số sai số, kết quả chỉ ra rằng, cả 2 mô hình đều có độ chính xác tương đối tương đồng. Cụ thể, theo Bảng 7, chỉ số MAE (Mean Absolute Error) của mô hình MIDAS là 1,394570, thấp hơn một chút so với GARCH với giá trị 1,408172. Điều này cho thấy, mô hình MIDAS có lợi thế nhỏ hơn về mặt sai số tuyệt đối trung bình. Tuy nhiên, với chỉ số RMSE (Root Mean Square Error), mô hình GARCH lại có hiệu quả tốt hơn khi đạt giá trị 2,305803, thấp hơn đôi chút so với MIDAS là 2,318583. Chỉ số RMSE phản ánh khả năng mô hình xử lý các sai số lớn và kết quả này cho thấy, mô hình GARCH ổn định hơn trong việc hạn chế các sai số lớn so với MIDAS.

Bảng 7: Thống kê chỉ số sai số

	MIDAS	GARCH
MAE	1,394570	1,408172
RMSE	2,318583	2,305803

Nguồn: Ước lượng của nhóm tác giả

Nhiều nghiên cứu trước đây từng ghi nhận rằng, tăng trưởng kinh tế của Việt Nam có đặc tính dai dẳng theo thời gian, tức là chịu ảnh hưởng của sự dao động của chính nó trong quá khứ nhiều hơn so với ảnh hưởng của các biến số vĩ mô khác (Hung, 2022). Mà tính dai dẳng này được phản ánh tốt hơn trong mô hình GARCH so với mô hình MIDAS, vì vậy, mô hình GARCH có thể cho ra kết quả dự báo có chỉ số RMSE thấp hơn.

Nhìn chung, cả 2 mô hình đều có ưu điểm và nhược điểm riêng, với mức chênh lệch giữa các chỉ số sai số là không đáng kể. Việc lựa chọn mô hình phù hợp sẽ tùy thuộc vào yêu cầu cụ thể của nhà nghiên cứu, chẳng hạn như: ưu tiên về khả năng dự báo chính xác các giá trị trung bình (MIDAS) hay xử lý hiệu quả các giá trị ngoại lệ (GARCH).

KẾT LUẬN

Nghiên cứu này tập trung vào việc dự báo tăng trưởng GDP của Việt Nam năm 2025 bằng cách áp dụng 2 mô hình dự báo nổi bật: GARCH và MIDAS. Kết quả phân tích cho thấy, GARCH là mô hình dự báo chính xác hơn trong bối cảnh hiện tại, nhờ vào khả năng nắm bắt các yếu tố chu kỳ và xu hướng dữ liệu một cách hiệu quả. Mô hình GARCH sử dụng các yếu tố lịch sử của dữ liệu để dự đoán các giá trị tương lai, điều này giúp cải thiện độ chính xác trong việc dự đoán các biến động kinh tế. Trong khi đó, mặc dù MIDAS cũng là một công cụ mạnh mẽ trong việc kết hợp dữ liệu với tần suất khác nhau, nhưng nó cho thấy, kém chính xác hơn trong việc dự đoán tăng trưởng GDP so với GARCH trong nghiên cứu này./.

TÀI LIỆU THAM KHẢO

1. Bollerslev (1986), Generalized Autoregressive Conditional Heteroskedasticity, Journal of Econometrics, 31(3), 307-327.

2. Engle (1982) Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation, Econometrica, 50(4), 987-1007.

3. Hung, L. D. (2022), Steady State Growth of Vietnam Economy, Southeast Asian Journal of Economics, 10(2), 35-58.

4. Lê Mai Trang, Hoàng Anh Tuấn, Nguyễn Thị Hiên, Đinh Thị Hà, Trần Kim Anh (2022) Ứng dụng mô hình MIDAS để dự báo tăng trưởng xuất khẩu của Việt Nam, Tạp chí Ngân hàng, truy cập từ https://tapchinganhang.gov.vn/ung-dung-mo-hinh-midas-de-du-bao-tang-truong-xuat-khau-cua-viet-nam-13382.html.

5. Lê Văn Tuấn và Phùng Duy Quang (2020), Áp dụng mô hình GARCH dự báo ảnh hưởng của đại dịch Covid-19 đến thị trường chứng khoán Việt Nam, Tạp chí Công thương, truy cập từ https://tapchicongthuong.vn/ap-dung-mo-hinh-garch-du-bao-anh-huong-cua-dai-dich-covid-19-den-thi-truong-chung-khoan-viet-nam-75518.htm

6. Nguyễn Thanh Hương và Bùi Quang Trung (2015), Ứng dụng mô hình kết hợp arima-garch để dự báo chỉ số vn-index, Tạp chí Khoa học và Công nghệ Đại học Đà Nẵng, số 4(89), 118-122.

7. Nguyễn Thanh Tùng và Phạm Thị Lan Anh (2022), Dự báo tăng trưởng GDP Việt Nam bằng mô hình MIDAS kết hợp dữ liệu tần suất cao, Tạp chí Nghiên cứu Kinh tế, 39(5), 67-79.

8. Nguyễn Thị Hiên và cộng sự (2022), Ứng dụng mô hình ARCH, GARCH phân tích độ biến động của hợp đồng tương lai VN30F1M trên thị trường chứng khoán phái sinh Việt Nam, Tạp chí Ngân hàng, truy cập từ https://tapchinganhang.gov.vn/ung-dung-mo-hinh-arch-garch-phan-tich-do-bien-dong-cua-hop-dong-tuong-lai-vn30f1m-tren-thi-truong-chung-khoan-phai-sinh-viet-nam-10638.html.

9. Phùng Duy Quang và cộng sự (2024), Ứng dụng mô hình arch và garch dự báo giá gạo tại Thái Lan, FTU Working Paper Series, truy cập từ https://fwps.ftu.edu.vn/2024/07/22/ung-dung-mo-hinh-arch-va-garch-du-bao-gia-gao-tai-thai-lan/.

10. Trần Minh Quân (2021), Ứng dụng mô hình MIDAS để dự báo lạm phát ở Việt Nam, Tạp chí Tài chính, 29 (2), 112-124.

Ngày nhận bài: 06/01/2025; Ngày phản biện: 15/01/2025; Ngày duyệt đăng: 18/01/2025

[1] Bài viết là một sản phẩm của đề tài cấp Bộ “Những vấn đề kinh tế thế giới và Việt Nam năm 2025” do TS. Lý Đại Hùng làm chủ nhiệm, Viện Kinh tế Việt Nam chủ trì thực hiện.